🌎Mineria.Space🚀

Blog

  • Modelado de Vetas con muestras de canales usando Leapfrog Geo

    Modelado de Vetas con muestras de canales usando Leapfrog Geo

    Esto está escrito para aquellos que tienen problemas para modelar vetas con datos fragmentados, especialmente muestras de canales.

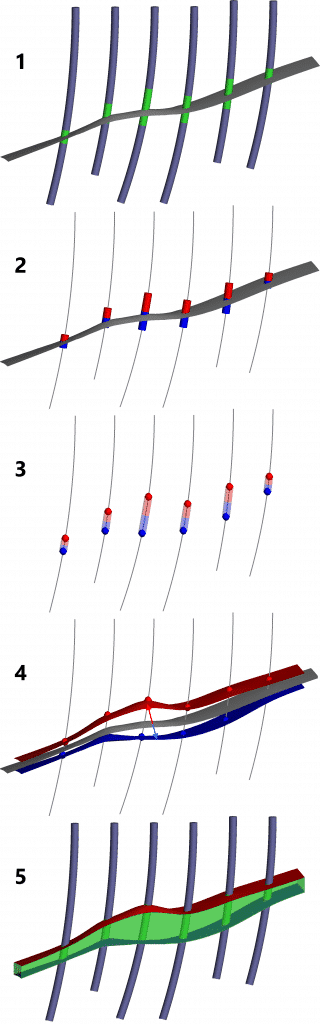
    La herramienta de vetas de Leapfrog Geo fue diseñada para trabajar con datos de sondajes, idealmente perforaciones que intersecan ambas paredes de la estructura de veta tabular. Si está utilizando la herramienta de modelado de vetas con datos de muestra de canal fragmentados, encontrará útiles estos consejos y trucos. Cómo funciona la herramienta de vetas Para empezar, vale la pena comprender cómo funciona la herramienta de vetas. Consulte la figura 1 a continuación.

    1. Primero, se genera una superficie de referencia a partir de los puntos medios de los intervalos de las vetas.
    2. A los segmentos de veta se les asignan lados de pared colgante (HW) y pared de pie (FW) según su orientación a la superficie de referencia.
    3. Se generan puntos HW y FW separados en los extremos de estos segmentos.
    4. Se generan las superficies HW y FW; ambas son compensaciones de la superficie de referencia que se ajustan a los puntos respectivos.
    5. El producto final es el volumen encerrado entre las superficies HW y FW.

    Clasificación del segmento de veta

    Debido a la forma en que Leapfrog Geo clasifica automáticamente los segmentos de vetas, podemos definir tres tipos básicos de muestras de vetas.
    • Las muestras de pared a pared están en el mismo agujero o canal y representan / tocan / intersecan ambas paredes de la verdadera estructura de la veta.
    • Las muestras de vetas incompletas son muestras que representan solo una pared de la verdadera estructura de la veta.
    • Las muestras de vetas internas no se cruzan con ninguna de las paredes verdaderas de la vena.


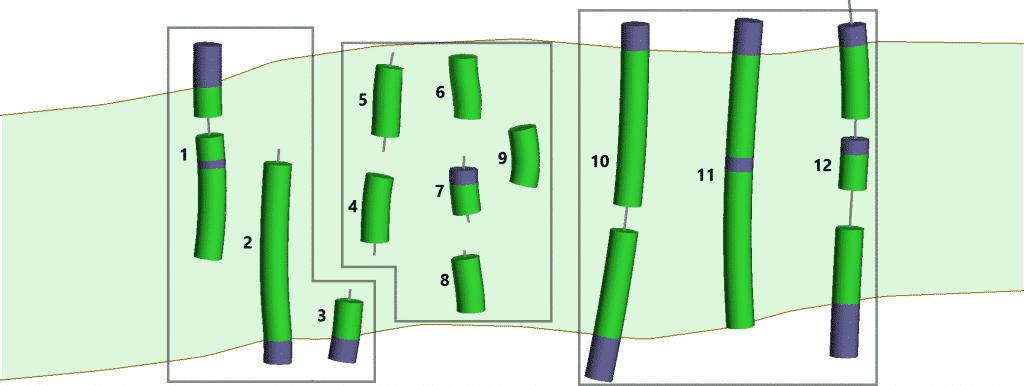
    Figura 2. Grupos: Derecha = muestras de pared a pared, Izquierda = muestras incompletas, Centro = muestras internas

    La estructura de la veta ‘verdadera’ está representada por el color verde claro, con las paredes representadas por las líneas marrones. Los intervalos verdes representan muestras de vetas registradas, los intervalos violetas representan muestras de «vetas externas» registradas, las líneas grises representan las secciones no muestreadas del pozo o canal.

    Como puede ver en las figuras 3 y 4, la clasificación automática de segmentos de vetas de Leapfrog Geo hace un buen trabajo con tipos de muestras de pared a pared, incluso cuando están muy fragmentadas como el último hoyo, pero no funciona tan bien con los tipos de muestra incompletos y tipos de muestras internas. Estos tipos de muestras internas e incompletas pueden producir triangulaciones superficiales deficientes porque las superficies están en contacto con cada uno de sus respectivos puntos finales de segmento. Las superficies de la pared colgante y la pared del pie pueden cruzarse entre sí, generando agujeros en el volumen modelado de la veta.

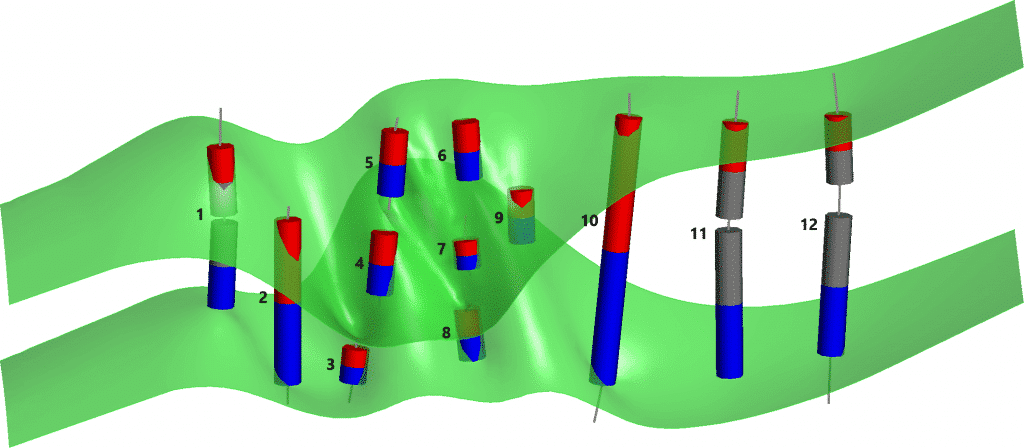
    Figura 3. Resultados de la clasificación automática de segmentos de vetas de Leapfrog Geo. Cada extremo de segmento está representado por uno de estos tres tipos: Muro colgante (rojo), Muro de pie (azul) y Excluido (gris). Las triangulaciones de la superficie de la pared de la vena resultantes son verdes en esta imagen.

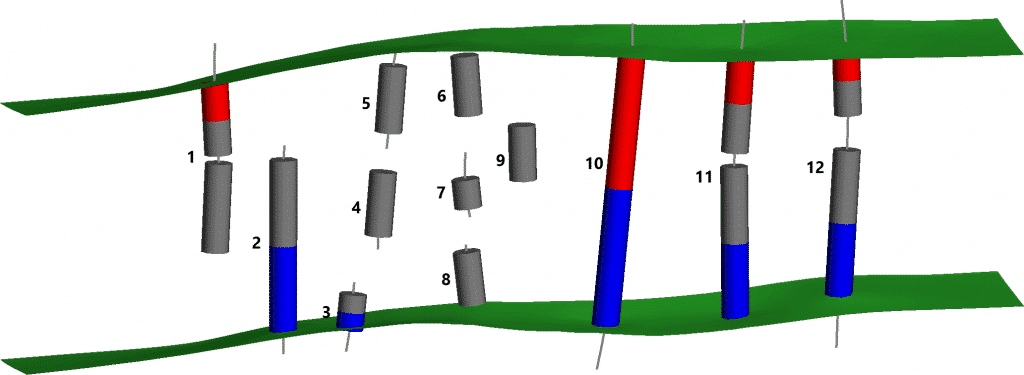
    Figura 4. La clasificación ideal de estos segmentos de vetas. Todas las muestras internas se clasifican como «Excluidas». Se excluyen los extremos internos de los segmentos incompletos.

    Edición manual

    Con algunas ediciones manuales, puede lograr la clasificación de segmento de vena ideal en Leapfrog Geo.

    Editar segmentos de vetas

    Para corregir los segmentos de vena en las muestras incompletas, deberá editar manualmente los segmentos de vena y anular sus clasificaciones automáticas. Haga clic con el botón derecho en los segmentos de la vena y seleccione Editar en escena (ver figura 5).

    Figura 5. Para editar segmentos de vena, haga clic con el botón derecho en el objeto de segmentos de vena debajo de la vena en el árbol del proyecto.

    Haga clic en un segmento de vena, luego en el cuadro de diálogo Orientaciones de segmento de vena desmarque Auto para el punto (A o B) que es incorrecto. Fije el punto a la clasificación correcta. En el ejemplo ilustrado en la figura 6, el punto A del segmento parcial ha sido excluido por lo que será ignorado por las superficies de la pared de la veta. Repita esto para todos los segmentos de vena clasificados incorrectamente de muestras parciales.

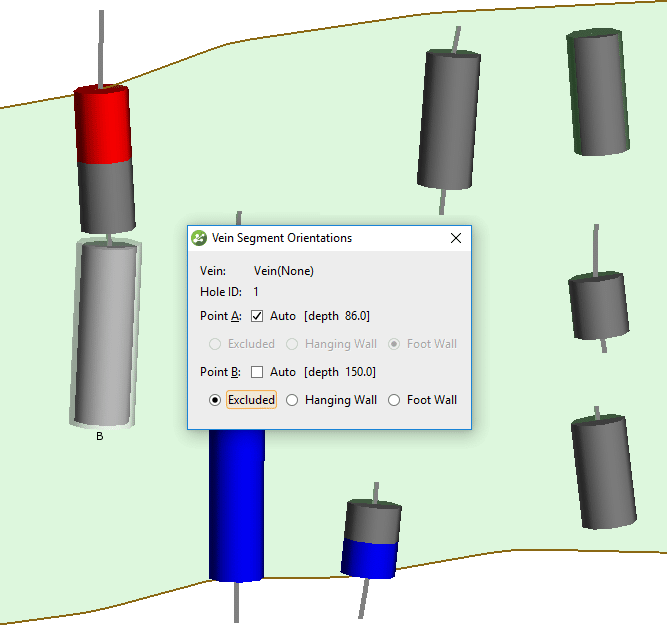
    Figura 6. Anule manualmente la clasificación de segmentos de vetas.

    Ignorar muestras internas

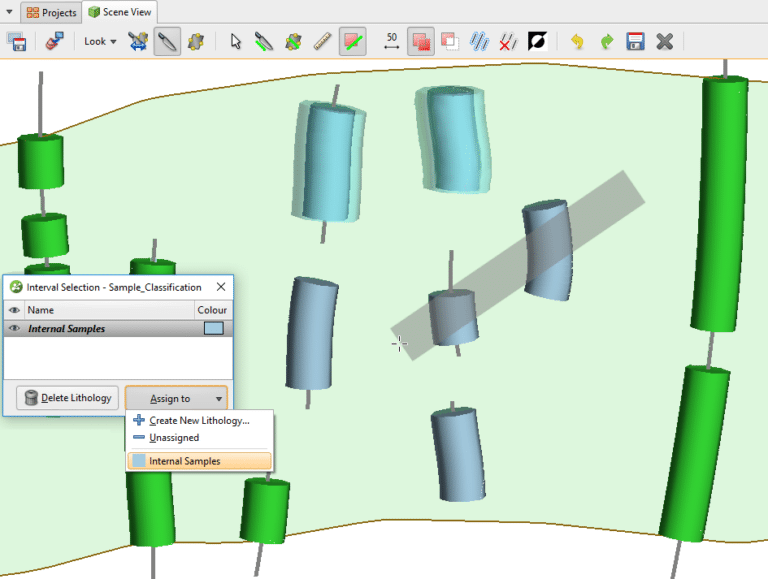
    Puede llevar mucho tiempo anular manualmente la clasificación del segmento de vena, especialmente con muestras de vetas internas que deben tener ambos extremos de segmento (punto A y punto B) excluidos. Una forma de evitar esto es ignorar estas muestras con un filtro de consulta. Primero, deberá clasificar las muestras internas en la tabla de intervalos. Luego, cree una nueva selección de intervalo en la tabla de intervalos a partir de la cual se construyó su vena (consulte la figura 7).

    Seleccione y asigne todas las muestras internas a un nuevo código de ‘litología’ (ver figura 8)

    Una vez que se crea la columna de selección de intervalo, en la misma tabla de intervalo, cree un nuevo Filtro de consulta que ignore las muestras internas.

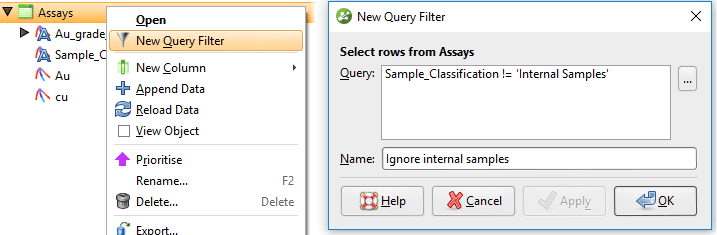
    Figura 9. Cree un nuevo filtro de consulta que ignore las muestras de vetas internas. Para aplicar este filtro de consulta a la vena, abra los segmentos de la vena, desmarque la opción para heredar el filtro de consulta del GM (modelo geológico) y seleccione el nuevo filtro de consulta de la lista desplegable

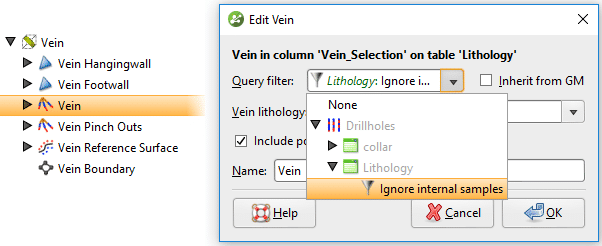
    Figura 10. Aplique un filtro de consulta a los segmentos de vena para ignorar las muestras internas.

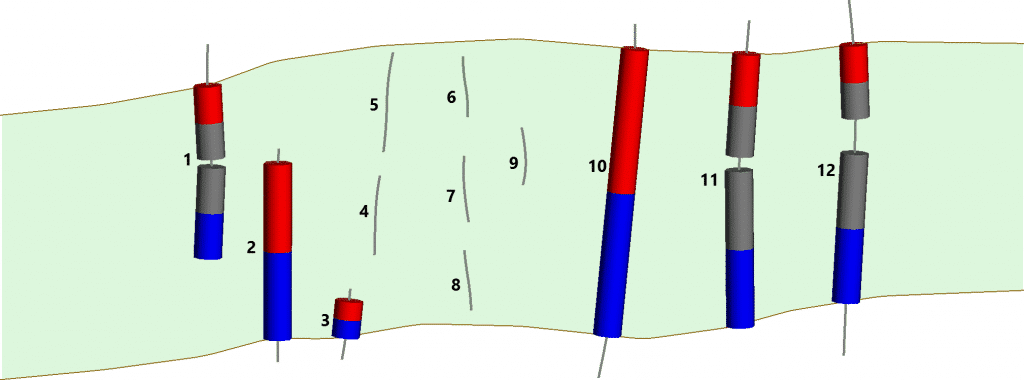
    Figura 11. Resultados de la clasificación de segmentos de vetas de Leapfrog Geo después de ignorar las muestras internas

    Ignorar puntos al final de los agujeros

    Dependiendo de los datos, es posible reducir el número de ediciones manuales excluyendo automáticamente los extremos del segmento al final de un agujero o canal. La configuración predeterminada para los segmentos de veta es incluir puntos al final de los agujeros. Para cambiar esta configuración, abra los segmentos de la vena haciendo doble clic (o haga clic con el botón derecho y seleccione Abrir), resaltados en naranja en la imagen, luego desmarque la opción para incluir puntos en los extremos de los agujeros (ver figura 12).

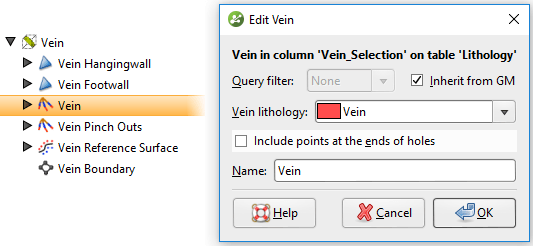
    Figura 12. Desmarque la opción para incluir puntos en los extremos de los agujeros.

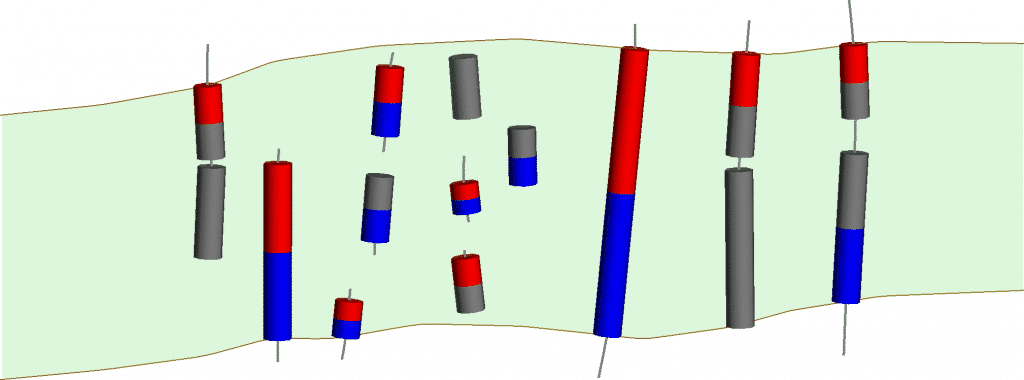
    Figura 13. La clasificación automática de segmentos de veta que excluye puntos en los extremos de los pozos.

    Como puede ver en la figura 13, los extremos de los segmentos de veta se excluyen al final de los orificios o canales. Esto ha resuelto el problema de clasificación de algunas de las muestras internas e incompletas. Sin embargo, si hay muchas muestras de vetas que se extienden hasta el final de los orificios (p. Ej., El orificio 11), o si la vena representa un caparazón de grado que debe encerrar firmemente todas las muestras de vetas, es posible que cambiar este ajuste no siempre sea apropiado

    Conclusión

    Con respecto a la clasificación automática de segmentos de vetas de Leapfrog Geo, el tipo de muestra de veta más recomendado para usar es de pared a pared. Incluso si el muestreo de pared a pared está fragmentado (separado por intervalos no registrados o intervalos sin vetas), la clasificación automática de segmentos producirá resultados apropiados. Con las muestras de canal, si las muestras de vena se pueden incluir en el mismo canal continuo, perpendicular a la estructura de veta tabular, puede minimizar o eliminar la necesidad de ediciones manuales en Leapfrog Geo (figura 14).

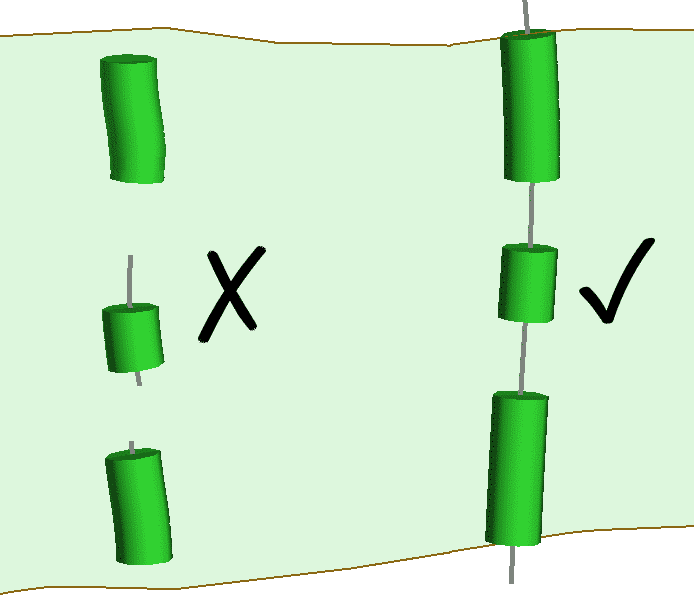
    Figura 14. Muestras de canales fragmentados. Las muestras de la izquierda deberán editarse manualmente para producir una triangulación de vena razonable, mientras que las muestras de la derecha funcionarán automáticamente

    Fuente: Leapfrog Geo

  • Optimización Simultánea Con GEOVIA Whittle

    Optimización Simultánea Con GEOVIA Whittle

    RESUMEN

    Este documento describe la base técnica del módulo de Optimización Simultánea Avanzada (SIMO Avanzada) en GEOVIA Whittle ™. El módulo SIMO avanzado permite a los planificadores de minas crear programas óptimos a largo plazo para la operación de minas a cielo abierto. 1 SIMO avanzado utiliza el motor ProberB que se desarrolló por Whittle Development Pty Ltd. El método para encontrar el programa óptimo se descompone en tres pasos: 1) agregar bloques en retrocesos, paneles y contenedores de mezcla para reducir el tamaño del problema; 2) expresar el problema de programación en un sistema lineal que se puede resolver mediante programación lineal y utiliza un enfoque iterativo para encontrar un horario óptimo; y 3) iterar de forma semialeatoria a través del espacio de la solución para asegurar que el programa obtenido esté cerca de la solución óptima.

    INTRODUCCIÓN

    Los métodos tradicionales utilizados en la planificación estratégica de minas tienden a optimizar un parámetro a la vez, mientras que la Optimización Simultánea Avanzada (SIMO Avanzada) considera todos los parámetros y alternativas simultáneamente, por lo que proporciona una solución casi óptima. Soluciones anteriores que utilizaban Milawa para la optimización del cronograma, Stockpile & Cut-off Optimization (SPCO) para la optimización de cut-off, y múltiples escenarios de mezclas extractivas para optimizar la mezcla se reemplazan mediante el uso de Advanced SIMO, que optimiza todos estos parámetros para maximizar las ganancias.

    La optimización tradicional de pit shell (Lerch-Grossman o Pseudoflow) todavía es necesaria para crear pit shell óptimo. Los pit shell son en su mayoría independientes del cronograma y el almacenamiento y, por lo tanto, se pueden realizar independientemente de una optimización SIMO avanzada. Si bien se podría argumentar esta afirmación, las restricciones de pendiente y la economía siguen siendo, con mucho, los principales impulsores de la forma del pit Shell en el cronograma.

    Una ejecución de optimización simultánea (SIMO) optimizará uno y solo un escenario de la estrategia de retroceso. Si se desea optimizar la selección y la estrategia de retroceso, esa optimización podría realizarse por separado utilizando el selector de retroceso, o mejor, con suficientes recursos informáticos evaluando manualmente las diferentes estrategias, a través del análisis de la piel, por ejemplo.

    A partir de un conjunto de parámetros de entrada (modelo de bloque, restricciones económicas y mineras, etc.), un usuario desea calcular un programa que maximice las ganancias a través del valor actual neto (VPN). El VPN se formula en función de esos parámetros de entrada, el programa y todas las demás variables. El cronograma es la variable que tiene más grados de libertad y tiene el mayor impacto en el VPN. El cronograma proporciona una descripción de qué bloque extraer y cuándo con el detalle de sus destinos (es decir, si se va a procesar, almacenar o descartar). Encontrar el plan de mina óptimo se puede reducir básicamente a encontrar el cronograma óptimo.

    El programa óptimo para una mina se puede describir con un conjunto de ecuaciones lineales e inecuaciones con una función objetivo que representa el VPN después de la vida de la mina. El objetivo de la optimización es resolver todas las variables y parámetros de entrada que maximizan la función objetivo. Si dicho sistema es lineal y lo suficientemente pequeño, se puede resolver utilizando un solucionador de programación lineal (LP) tradicional y se garantiza una solución óptima. Desafortunadamente, en el caso de la mayoría de los programas de mina, el sistema no es ni lo suficientemente pequeño ni lineal.

    ¿POR QUÉ LA OPTIMIZACIÓN SIMULTÁNEA ES MEJOR QUE LOS MÉTODOS TRADICIONALES?

    La suposición básica que se hace al optimizar un parámetro por separado de otros es que los parámetros son independientes entre sí. Por ejemplo, la optimización de corte supone que las leyes de corte se pueden optimizar independientemente del cronograma. Sin embargo, cambiar el límite a menudo significa que el programa que alguna vez fue óptimo puede no serlo para un límite diferente.

    Cuando se optimiza en pasos separados, una decisión tomada en una etapa temprana (por ejemplo, Programa en la Figura 1) impacta las decisiones posteriores, por lo tanto, reduce o enmascara las posibilidades de una mejor solución por completo.

    Las siguientes secciones, Pasos 1 al 3, describirán brevemente la lógica para derivar un cronograma de minería óptimo con SIMO.

    PASO 1: AGREGACIÓN PARA “BLEND BINS”

    La descripción de este problema de programación en un sistema de ecuaciones es demasiado grande para que la resuelva cualquier computadora. Para reducir el tamaño del sistema, GEOVIA Whittle utiliza «contenedores de mezcla» como metodología de agregación. Dado que los bloques que tienen grados de material similares tendrán un resultado similar, agregar esos bloques reducirá significativamente el tamaño del problema sin afectar los resultados (a expensas de la entrada adicional del usuario para especificar los contenedores de mezcla).

    Los pits se subdividen en retrocesos (pushbacks) y en bancos (benches). Un panel designa un banco específico dentro de un retroceso (ver Figura 2), y los bloques de un retroceso y un banco específicos se asignan a un panel. La definición de contenedores de mezcla permitirá agrupar los bloques de un panel que tienen características de grado similares en un solo contenedor (Figura 3).

    El usuario define los contenedores de mezcla especificando el rango de grado para cada contenedor. Tenga en cuenta que los rangos de grado del depósito, si se eligen incorrectamente, tendrán un impacto significativo en la optimización. Proporcionar suficientes contenedores de mezcla alrededor de los límites sensibles es fundamental para el proceso. Los usuarios generalmente comienzan con un mayor número de contenedores de mezcla para determinar dónde se encuentra el límite de mineral o desmonte, qué grupos de contenedores se procesan, almacenan o recuperan juntos, y luego los consolidan para que los contenedores se conviertan en clases de materiales para la programación.

    Una vez que los bloques se han agregado a pushback, panel y contenedores, el tamaño del sistema ahora se reduce a un tamaño aceptable. El beneficio adicional de subdividir por retroceso (pushback) y panel es que la estructura ahora puede seguir implícitamente las restricciones mineras relacionadas con el perfil de la pendiente y la precedencia del bloque.

    PASO 2: ENCONTRAR UNA SOLUCIÓN ÓPTIMA

    Para describir el enfoque, echemos un vistazo primero al caso sin existencias.

    Caso sin stockpile

    Un cronograma puede expresarse mediante un vector Xi, j que especifica la profundidad total extraída para el retroceso iy el período j, de modo que, para cada período de un cronograma, se puede saber cuánto de cada retroceso se extrae. Por ejemplo, en un caso simple de un pozo con un retroceso, seis bancos y tres períodos, el vector X = (0.5, 3.2, 5.8) indica que al final del período 1, la mitad del primer banco (banco 0) es minado; al final del período 2, la minería alcanzó el 20% del cuarto banco (banco 3); y al final del período 3 sólo queda el 20% del último banco.

    Si el problema del cronograma se expresa utilizando el principio anterior mientras se agregan restricciones de minería, mezcla y procesamiento, la resolución de Xi, j proporcionará la solución óptima para el problema.

    Sin embargo, el sistema no se puede resolver como está. Debe ser lineal para que se pueda resolver con los solucionadores LP tradicionales. Si los bancos y los retrocesos que se extraerán dentro de cada período son fijos, se puede hacer que el sistema sea lineal y encontrar el programa óptimo para este caso específico utilizando un solucionador de LP.

    El solucionador de LP podrá calcular cuál es la fracción óptima del banco para extraer.

    En nuestro ejemplo anterior, si (0.5, 3.2, 5.8) fuera un cronograma óptimo, esa solución se habría encontrado cuando arreglaríamos el banco 0 para el período 1, el banco 3 para el período 2 y el banco 5 para el período 3. En otras palabras, al proporcionar el valor inicial X = (0, 3, 5), el solucionador podrá encontrar la solución óptima (0.5, 3.2, 5.8) para ese caso. Arreglar los bancos y los retrocesos a la mía en cada período es una limitación seria, y no es práctico ni útil solicitar que información del usuario. Dado que el usuario no sabe a priori qué bancos y retrocesos extraer dentro de cada período, uno tendría que iterar a través de todas las combinaciones de bancos y retrocesos que se pueden extraer en todos los períodos para encontrar la solución óptima. En el ejemplo anterior, con un retroceso, cinco bancos y tres períodos, el software necesitaría iterar a través de 56 combinaciones.2 Ese número crecerá exponencialmente a medida que se agreguen más retrocesos, bancos y períodos. Con solo 10 bancas, 10 períodos y 5 retrocesos, el número de combinaciones se acerca a 6,7 ​​× 10 24, por lo que, para un problema de tamaño normal, esto produce demasiadas combinaciones para evaluar. Para resolver este problema, se utiliza un enfoque iterativo análogo al método de Newton (Recetas numéricas. El arte de la computación científica, 3ª edición, 2007) para encontrar un óptimo local (consulte la Figura 4 en la página siguiente).

    Como se muestra en la Figura 4, a partir de cualquier solución factible inicial (el conjunto fijo de bancos y retrocesos para extraer para cada período), el solucionador de LP calcula el programa óptimo; si la solución está dentro de los límites del programa inicial (es decir, no ha alcanzado los límites de los bancos y los retrocesos que se arreglaron), entonces el programa ha encontrado un máximo local; de lo contrario, el programa reinicia el proceso utilizando esta última solución como una solución inicial factible para la siguiente iteración. Este proceso puede comenzar desde cualquier solución inicial factible, permitiendo encontrar un máximo local en el espacio de la solución.

    Caso con Stockpile

    El uso de existencias agrega un nivel de complejidad al algoritmo general. Es decir, el sistema de ecuaciones descrito anteriormente vuelve a ser no lineal. Las variables de entrada agregadas que se necesitan para las existencias requerirán cambiar las restricciones de ley y tonelaje, y deberán expresarse como un producto de dos variables (por ejemplo, ax1x2 +… = k, donde x1 y x2 representan la ley de la pila y la cantidad de material que sale de la reserva, respectivamente). El sistema ahora es cuadrático no convexo y no se puede resolver con un solucionador de LP. Entonces, el enfoque adoptado es resolver por separado las leyes de las pilas y los movimientos de las pilas. Primero, las leyes de la reserva (x1) se estiman iterativamente; luego, el grado de la pila se fija para permitir que el solucionador de LP resuelva el programa.

    Tenga en cuenta que este enfoque no optimiza las leyes de la pila de existencias y el cronograma juntos, por lo que las leyes de la pila de existencias pueden no ser óptimas para el cronograma. Sin embargo, dado que muchos bloques contribuyen a las reservas, la calidad de la pila no tiende a cambiar significativamente con el cronograma.

    Este enfoque es una mejora significativa en comparación con SPCO, que solo optimiza las leyes de corte. Aquí, el movimiento del material de la pila y las calidades de la pila se optimizan para ofrecer el mejor VAN posible.

    PASO 3: ENCONTRAR LA SOLUCIÓN ÓPTIMA

    El enfoque iterativo descrito anteriormente no garantiza que la solución encontrada sea la solución óptima. La Figura 5 ilustra el concepto en el que partir de diferentes programas iniciales factibles puede conducir a diferentes máximos locales, y ese enfoque podría devolver un máximo local en lugar de la solución óptima.

    Utilizando un método análogo al método de Monte-Carlo, el procedimiento se repite un gran número de veces a partir de diferentes soluciones factibles iniciales. Como un alpinista que llega a la cima de un pico, solo para descubrir que estaban rodeados por otros puntos más altos de la montaña, este método coloca a muchos alpinistas al azar a través de la cordillera y la solución final se obtiene del escalador que llega a la cima en la cima más alta. cima.

    Se ha tenido cuidado para asegurar que el espacio de solución completo se muestrea aleatoriamente para que se encuentren todos los máximos locales. Las iteraciones se pueden dejar durante mucho tiempo, sin embargo, la velocidad a la que se encuentra un mejor máximo disminuye rápidamente y el algoritmo se detiene cuando la posibilidad de encontrar una solución significativamente mejor se vuelve muy improbable. (Ver Figura 6.)

    CONCLUSIÓN

    El enfoque de optimización simultánea avanzada de GEOVIA Whittle puede encontrar mejores resultados en comparación con los métodos tradicionales. Hemos demostrado que el plan de mina óptimo para un problema a cielo abierto se puede reducir a encontrar el cronograma óptimo mediante la optimización de mezclas, acopios y estrategias de procesamiento dentro de un enfoque iterativo. El algoritmo consiste en iterar a través del espacio de posibles horarios para encontrar el casi óptimo horario que obedece a las limitaciones de minería y procesamiento.

    *this is a traslation of original article «GEOVIA-Whittle-SIMO-WhitePaper»

  • Los volcanes del Anillo de Fuego del Pacífico

    Los volcanes del Anillo de Fuego del Pacífico

    Los volcanes del Anillo de Fuego del Pacífico

    Un volcán puede definirse como una abertura en la corteza terrestre a través de la cual el magma caliente (roca fundida rica en gas) de debajo de la corteza llega a la superficie (Tazieff y Sabroux, 1983). Con frecuencia, los gases interrumpen el magma y arrojan los grupos de rocas de varios tamaños resultantes a la atmósfera (o, en el caso de los volcanes submarinos, al agua). Estos escombros vuelven a caer alrededor del respiradero eruptivo y se acumulan para formar una colina alrededor del cráter en erupción. Al mismo tiempo, se vierte magma fundido, desgasificado (o originalmente pobre en gas) como la lava fluye. Estos flujos pueden, dependiendo de su viscosidad, la pendiente del suelo y el volumen de salida, alcanzar distancias variables desde el respiradero (desde unos pocos metros hasta más de 100 km) antes de solidificarse en roca.

    ¿Quieres Saber más sobre Volcanes?

    Accede a nuestro curso «Introducción a la Vulcanología Física»

    Acceder Ahora!!!

    La ubicación de los volcanes está estrechamente relacionada con los límites de las placas tectónicas. La mayoría de los volcanes del mundo se encuentran a lo largo de los límites de las placas convergentes (las zonas de subducción), las zonas de ruptura de las placas o los límites de las placas divergentes (las zonas de expansión). De hecho, dos tercios de los volcanes del mundo están situados a lo largo del límite de la placa del Pacífico, el llamado «Anillo de fuego» (Blong, 1984). A medida que la placa del Pacífico es empujada hacia el manto terrestre, se deshidrata y la roca fundida se eleva a través de la corteza continental suprayacente para formar volcanes en la zona de subducción (Fig. 1.1). Los volcanes de la zona de subducción son de especial interés porque, si bien no entran en erupción con tanta frecuencia y durante tanto tiempo como los volcanes de la zona de rift o expansión, producen las erupciones más explosivas y generalmente se encuentran en áreas densamente pobladas, como en el archipiélago de Indonesia. Otros volcanes bien conocidos, como la cadena de islas de Hawai, se producen debido a la ubicación de un punto caliente en las profundidades del manto terrestre, que alimentan de magma a la superficie a través de la placa suprayacente.

    Los volcanes aparecen en diferentes formas y tamaños, y se clasifican como activos, inactivos o extintos. Sin embargo, esta clasificación se basa en registros obtenidos durante muy poco tiempo, en términos geológicos, y puede ser engañosa porque los volcanes oficialmente extintos pueden volverse repentinamente activos después de varios cientos o incluso miles de años de reposo. Las erupciones del monte. Lamington en Papua Nueva Guinea (1951), Mt. Arenal en Costa Rica (1968) y Helgafell en Islandia (1973) son ejemplos de tal comportamiento (Tazieff & Sabroux, 1983). Como los registros históricos sugieren que más de 1300 volcanes separados han hecho erupción en algún lugar de la tierra en los últimos 10,000 años, todos los volcanes que muestran alguna actividad durante este período se identifican como volcanes históricamente activos o del Holoceno (Simkin y Siebert, 2000).

    El tamaño de una erupción volcánica se puede estimar de varias formas. Por ejemplo, por el volumen total de productos erupcionados (magnitud), por la tasa volumétrica o de masa a la que estos productos salieron del respiradero (intensidad), por el área sobre la cual se distribuyen los productos (poder dispersivo), por la violencia explosiva o por el potencial destructivo de la erupción (Blong, 1984). El índice de explosividad volcánica (VEI) introducido por Newhall y Self (1982) proporciona una medida descriptiva simple del tamaño de una erupción. Este índice combina el volumen total de material eruptivo, la altura de la nube eruptiva, la duración de la fase eruptiva principal y varios términos descriptivos en una escala logarítmica simple de explosividad creciente que va de 0 a 8. Es interesante notar que de todas las erupciones históricas, solo a la erupción de 1815 de Tambora (Indonesia) se le ha asignado un VEI de 7, mientras que no hay erupciones VEI 8 registradas. A la conocida y ampliamente documentada erupción del monte St. Helens (EE. UU.) En 1980 se le asignó un VEI de 5.

    Acceder Ahora!!!